こんにちは、くれあです。
今回は「3点を通る円の方程式」の求め方を紹介します。
基本的な解法と別解も紹介します、ぜひ参考にしてくださいね。
問題
問題
座標平面上において,3点\((2,1),(9,0),(10,7)\)を通る円\(O\)の中心と半径を求めよ.
解法①【一般形から求める】
最もメジャーな方法は円の一般形に3点の座標を代入して、
連立方程式を解いて円の方程式を求める方法です。
円の方程式の一般形
\(x^2+y^2+ax+by+c=0\)
(解答)
円\(O\)の方程式を\(x^2+y^2+ax+by+c=0\)とおくと,
3点\((2,1),(9,0),(10,7)\)を通るので
\(2a+b+c=-5\)・・・①
\(9a+c=-81\)・・・②
\(10a+7b+c=-149\)・・・③
①-②より\(-7a+b=76\)・・・④
③-②より\(a+7b=-68\)・・・⑤
⑤より\(a=-8b-68\).これを④に代入すると
\(49b+476+b=76\)
\(50b=-400\)
よって\(b=-8\)
\(a=-8b-68\)より,\(a=-12\),
\(a=-12\)と②より\(c=27\)
したがって円\(O\)の方程式は
\(x^2+y^2-12x-8y+27=0\)
変形して
\((x-6)^2+(y-4)^2=25\)
ゆえに,円\(O\)の中心は\((6,4)\),半径は5
解法②【標準形から求める】
また、解法①の最後に変形した標準形から
中心と半径を文字でおいて、連立方程式で導くこともできます。
円の方程式の標準形
\((x-p)^2+(y-q)^2=r^2\) (\(r>0\))
円の中心は\((p,q)\),半径はrとなりますね。
こちらの式からも連立方程式を作り円の方程式を求めることができます。
(解答)
円\(O\)の方程式を\((x-p)^2+(y-q)^2=r^2\)とおくと,
3点\((2,1),(9,0),(10,7)\)を通るので
\(p^2-4p+4+q^2-2q+1=r^2\)・・・①
\(p^2-18p+81+q^2=r^2\)・・・②
\(p^2-20p+100+q^2-14q+49=r^2\)・・・③
2乗が出てきて焦りますが、式同士を引くと消えてくれます.
①-②より\(14p-2q-76=0\),つまり\(q=7p-38\)・・・④
②-③より\(2p-68+14q=0\),つまり\(p=-7q+34\)・・・⑤
④に⑤を代入して
\(q=7p-38=7(-7q+34)-38=-49q+200\)
\(50q=200\)
\(q=4\),⑤より\(p=6\)
これらを②に代入して計算すると\(r^2=25\),すなわち\(r>0\)より\(r=5\)
ゆえに\((x-6)^2+(y-4)^2=25\)なので
円\(O\)の中心は\((6,4)\),半径は5
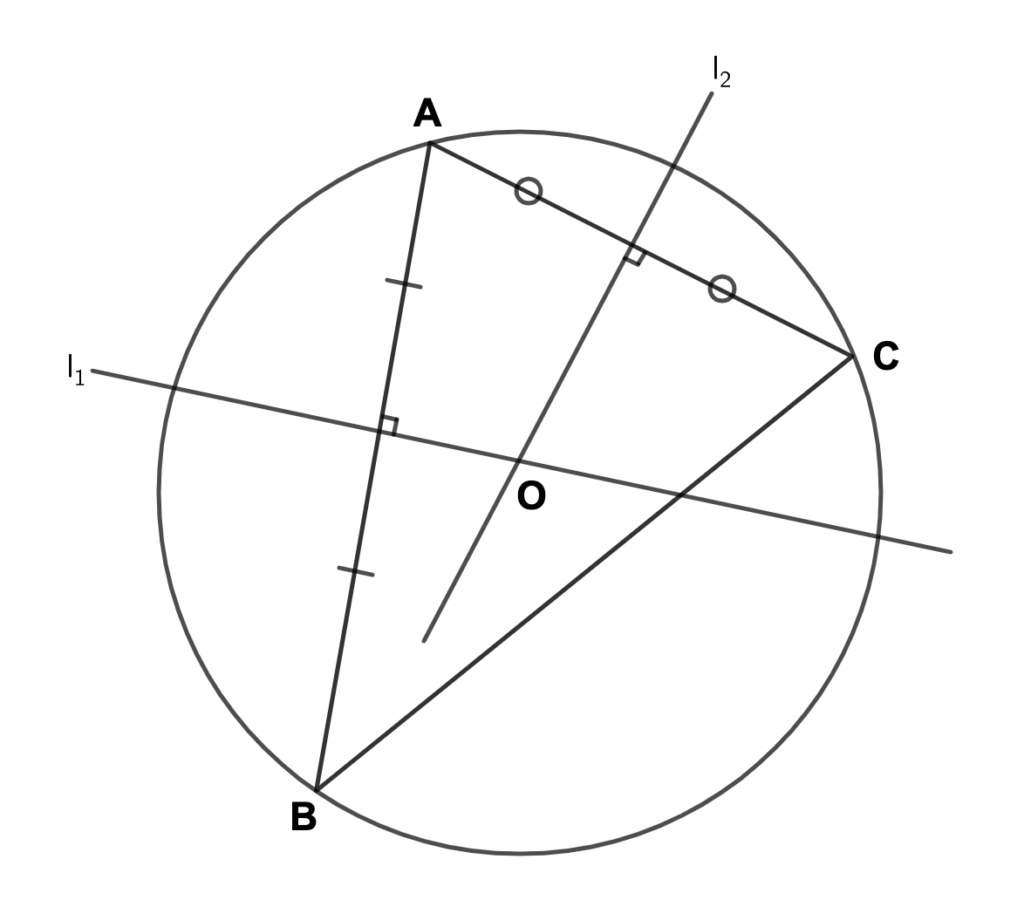
解法③【3点を頂点とする三角形の外接円と捉える】
3点\((2,1),(9,0),(10,7)\)を点\(A,B,C\)とすると
\(\triangle ABC\)の外接円となるので、その円の中心と半径を求めていきます。
方針としては\(AB,CA\)の垂直二等分線の直線を求め、その2直線の交点(=外接円の中心)を求めます。
三角形の垂直二等分線の交点が
外接円の中心となる!
(解答)
\(AB\)の垂直二等分線\(l_1\)を求める.
\(AB\)の中点は\(\bigl(\frac{11}{2}, \frac{1}{2}\bigr)\)
直線\(AB\)の傾きは\(-\frac{1}{7}\)なので\(l_1\)の傾きは\(7\)
よって\(l_1:y=7\bigl(x-\frac{11}{2}\bigr)+\frac{1}{2}\).
\(CA\)の垂直二等分線\(l_2\)を求める.
\(CA\)の中点は\(\bigl(6,4)\)
直線\(CA\)の傾きは\(\frac{6}{8}=\frac{3}{4}\)なので\(l_1\)の傾きは\(-\frac{4}{3}\)
よって\(l_2:y=-\frac{4}{3}\bigl(x-6\bigr)+4\).
\(l_1,l_2\)の交点を求める.
$$
\begin{align*}
7\Bigl(x-\frac{11}{2}\Bigr)+\frac{1}{2}&=-\frac{4}{3}\Bigl(x-6\Bigr)+4\\
-8(x-6)+24&=7(6x-33)+3\\
-8x+48+24&=42x-231+3\\
50x&=300\\
x&=6\\
y&=7\Bigl(6-\frac{11}{2}\Bigr)+\frac{1}{2}=4
\end{align*}
$$
よって\(l_1,l_2\)の交点は\((6,4)\),つまり求める円の中心は\((6,4)\)
あとは\((6,4)\)と3点のどれかの点との距離が半径になります。
\((6,4)\)と点C\((10,7)\)との距離は
\(\sqrt{(10-6)^2+(7-4)^2}=\sqrt{4^2+3^2}=5\)
よって半径は5
ゆえに円\(O\)の中心は\((6,4)\),半径は5
解法④【2曲線の交点を通る曲線の方程式を使う】
下記の方程式を用いて、上手く円の方程式を表します。
2曲線の交点を通る曲線の方程式
異なる2曲線\(f(x,y)\)と\(g(x,y)\)が交点をもつとき,
それらの交点を通る曲線の方程式は以下で表される.
$$
f(x,y)+kg(x,y)=0.\qquad(kは定数)
$$
ただし\(f(x,y)=0\)の場合は除く.
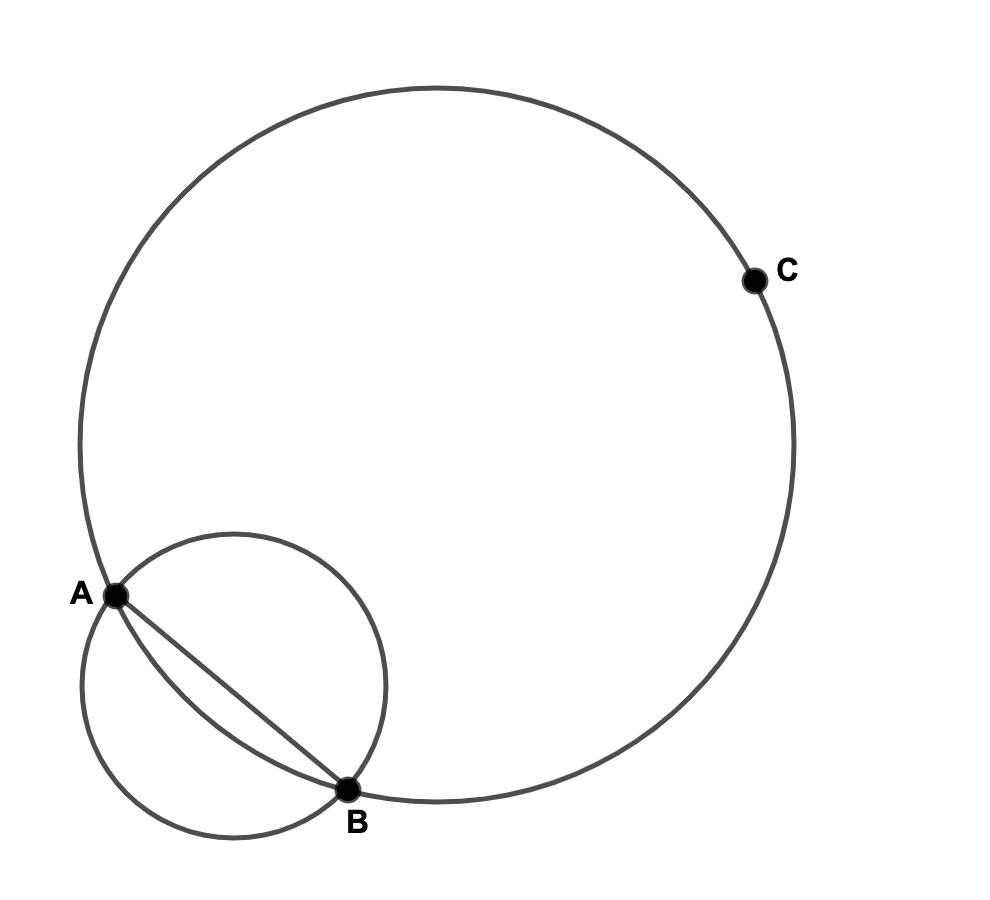
今回の問題では\(f(x,y)\)を2点\(A,B\)を直径とする円の方程式、
\(g(x,y)\)を同じ2点\(A,B\)を通る直線として計算します。
2点\(A,B\)を直径とする円上にある点を\(P(x,y)\)とすると
直径の円周角が直角であることから\(\vec{AP}\cdot\vec{BP}=0\)なので
2点\(A,B\)を直径とする円の方程式は
\(\vec{AP}\cdot\vec{BP}=(x-2)(x-9)+(y-1)(y-0)=0\)で表されます.
これらを使って求める円を簡単に計算することができます。
(解答)
2点\(A,B\)を直径とする円の方程式は
\((x-2)(x-9)+(y-1)y=0\)
直線\(AB\)の方程式は
\(y=-\frac{1}{7}(x-9)\)
変形して
\(x+7y-9=0\)となるので,\(AB\)を通る円は
\((x-2)(x-9)+(y-1)y+k(x+7y-9)=0\)
この円がC\((10,7)\)を通るので
\((10-2)(10-9)+(7-1)7+k(10+49-9)=0\)
\(8+42+50k=0\)
\(k=-1\)
よって求める円は
\((x-2)(x-9)+(y-1)y+(-1)(x+7y-9)=0\)
\(x^2-12x+y^2-8y+27=0\)
変形して
\((x-6)^2+(y-4)^2=25\)
ゆえに,円\(O\)の中心は\((6,4)\),半径は5
補足
因みに、点\(C,A\)で同様の方法で求めると、
\(k=0\)なので\(CA\)が直径で
\(CA\)が直径である円が求める円であることが分かります。
(解答)
直線\(CA\)の方程式は
\(y=\frac{3}{4}(x-2)+1\)
変形して
\(3x-4y-2=0\)となるので,\(CA\)を通る円は
\((x-2)(x-10)+(y-1)(y-7)+k(3x-4y-2)=0\)
この円がB\((9,0)\)を通るので
\((9-2)(9-10)+(0-1)(0-7)+k(27-0-2)=0\)
\(7\cdot(-1)+(-1)\cdot(-7)+25k=0\)
\(k=0\)
よって求める円は
\((x-2)(x-10)+(y-1)(y-7)+0(3x-4y-2)=0\)
\(x^2-12x+20+y^2-8y+7=0\)
変形して
\((x-6)^2+(y-4)^2=25\)
ゆえに,円\(O\)の中心は\((6,4)\),半径は5




コメント